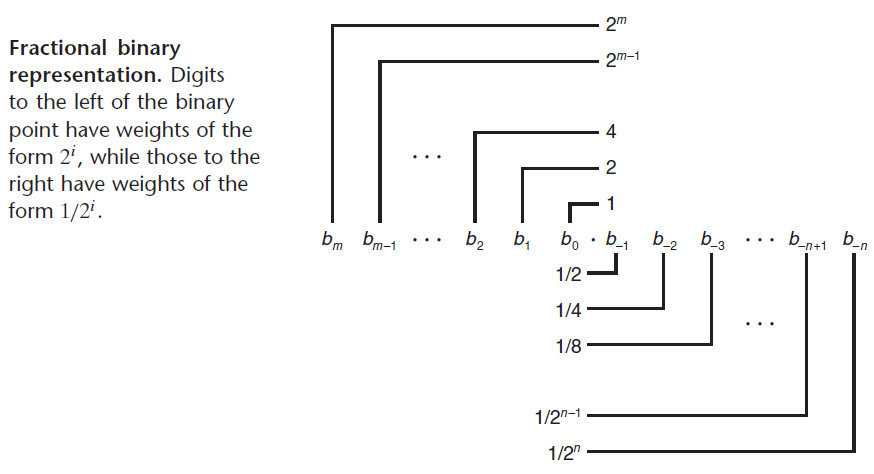
浮点表示对形如
的有理数进行编码。
直到 20 世纪 80 年代，每个计算机制造商都设计了自己的表示浮点数的规则，以及对浮点数执行运算的细节。另外，它们常常不会太多地关注运算的精确性，而把实现的速度和简便性看得比数字精确性更重要。
大约在1985 年，这些情况随着IEEE 标准754 的推出而改变了，这是一个仔细制订的表示浮点数及其运算的标准。这项工作是从1976 年开始由Intel 赞助的，与8087 的设计同时进行，8087 是一种为8086 处理器提供浮点支持的芯片。他们请William Kahan(加州大学伯克利分校的一位教授）作为顾问，帮助设计未来处理器浮点标准。他们支持Kahan加人一个IEEE 资助的制订工业标准的委员会。这个委员会最终采纳的标准非常接近于Kahan 为Intel 设计的标准。目前，实际上所有的计算机都支持这个后来被称为IEEE 浮点的标准。这大大提高了科学应用程序在不同机器上的可移植性。
IEEE浮点标准用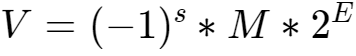
的形式来表示一个数：
① 符号(sign)，s决定这个数是负数(s=l)还是正数(s=0)，而对于数值0的符号位解释，作为特殊情况处理。
② 尾数(significand)，M是一个二进制小数，它的范围是1~2-
,或者是0~1-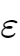
。
③ 阶码(exponent)，E的作用是对浮点数加权，这个权重是2的E次幂(可能是负数)。
E在后面所述的规格化和非规格化表示时有所区别。
将浮点数的位表示划分为三个字段，分别对这些值进行编码：
(1) 一个单独的符号位s，直接编码符号s。
(2) k位的阶码字段，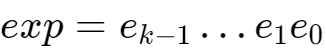
编码阶码E。
(3) n位小数字段，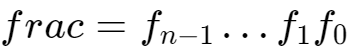
编码尾数M，但是编码出来的值也依赖于阶码字段的值是否等于0。
在单精度浮点格式（C 语言中的float)中，s、 exp 和 frac 字段分别为 1 位、k=8 位和 n=23 位，得到一个 32 位的表示。
在双精度浮点格式(C 语言中的double)中，s、exp 和 frac 字段分别为 1 位、k=11 位和 n=52 位，得到一个64 位的表示。
阶码的值决定了这个数是规格化的、非规格化的或特殊值：
规格化的值的阶码字段被解释为以偏置(biased)形式表示的有符号整数。也就是说，阶码的值是E=e-Bias，其中e 是无符号数，是一个等于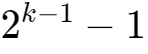
（单精度是127，双精度是1023）的偏置值。由此产生指数的取值范围，对于单精度是-126~+127, 而对于双精度是-1022~+1023。尾数定义为M=1+f。
当阶码域为全0时，所表示的数是非规格化形式。在这种情况下，阶码值是E=1-Bias，而尾数的值是M=f，也就是小数字段的值，不包含隐含的开头的1。
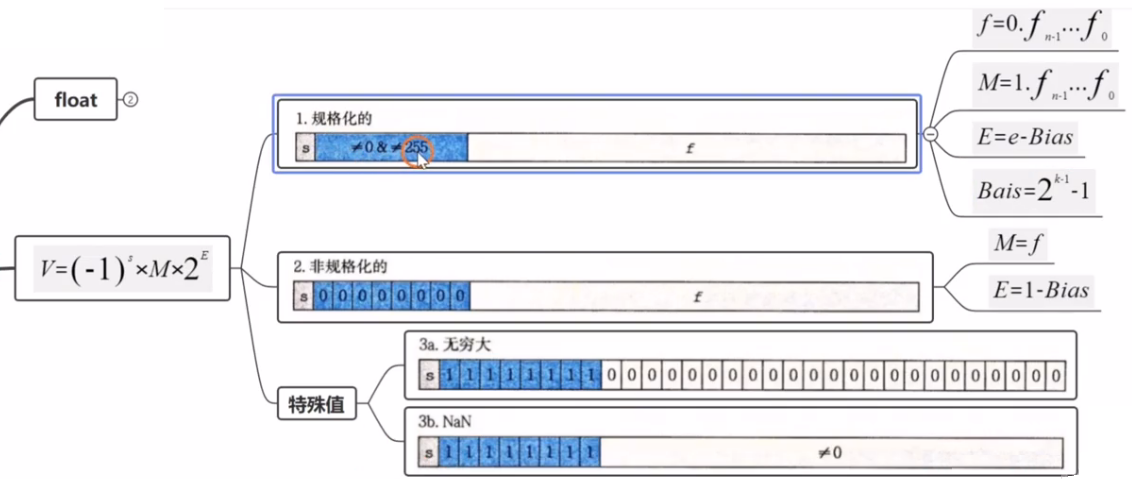
使阶码值为1- Bias 而不是简单的-bias 似乎是违反直觉的。这种方式提供了一种从非规格化值平滑转换到规格化值的方法。
6 位浮点格式可表示的值（k=3的阶码位和 n=2的尾数位。偏置量是 3：
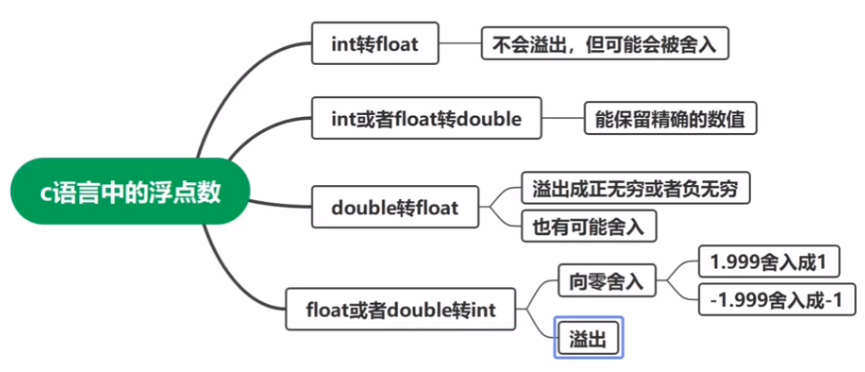
需要注意的是，浮点数加法和乘法不满足结合律 ，也不满足乘法对加法的分配律，以下举例说明：
(3.14+1e10)-1e10 = 0, // 3.14因为精度被略掉了
3.14+(1e10-1e10) = 3.14，
(1e20 *1e20) * 1e-20= inf,
1e20 * (1e20 * 1e-20)= 1e20
1e20 * (1e20 - 1e20)= 0.0,
1e20 * 1e20 - 1e20 * 1e20 = NaN
这些特殊的数学性质对于科学计算程序员和编译器的优化限制都具有重要意义，举例如下：
x = a + b + c;
y = b + c + d;
// 编译器可能试图通过产生下列代码来省去一个浮点加法
t = b + c;
x = a + t;
y = t + d;
// 但是对x来说，这个计算可能会产生于原始值不同的值,因为它使用了加法运算的不同结合方式浮点数的加减运算分为五步：
如有
X = 0.1011×2^3
Y = 0.1001×2^4
3.1 对阶
对阶是指对齐小数位，遵循“小阶向大阶看齐”的原则，以便结果的精度更高。
对阶还是比较好理解的。把指数小的数（X）的指数（3）转化成和指数高的数（Y）的指数（4）相等，同时指数小的数（X）的尾数的符号位后边补两个数指数之差的绝对值个（1个）0。对于本例来说，就是把X变为：
X = 0.01011 ×2^4
3.2 尾数相加减
按照例子来说，尾数相加减：
00 . 0 1 0 1 1
+
0 . 1 0 0 1 （注意看是怎么对齐的）
等于
00 . 1 1 1 0 1
这是相加，相减是把减数换成对应的补码再做相加运算即可。
3.3 规格化
不满足规格化的尾数进行规格化处理。当尾数发生溢出可能（尾数绝对值大于1）时，应调整阶码。
当出现以下两种情况时需要进行规格化。
① 两个符号位不相同，右规：两个符号位不同，说明运算结果溢出。此时要进行右规，即把运算结果的尾数右移一位。需要右规的只有如下两种情况：01××××和10××××。01×××右移一位的结果为001×××；10××××右移一位的结果为110×××。最后将阶码（指数）+1。
② 两个符号位相同，但是最高数值位与符号位相同，左规：两个符号位相同，说明没有溢出。此时要把尾数连续左移，直到最高数值位与符号位的数值不同为止。需要左规的有如下两种情况：111×××和000×××。111×××左移一位的结果为11×××0；000×××左移一位的结果为00×××0。最后将阶码（指数）减去移动的次数。
3.4 舍入
执行右规或者对阶时，有可能会在尾数低位上增加一些值，最后需要把它们移掉。比如说，原来参与运算的两个数（加数和被加数）算上符号位一共有6个数，通过上边三个操作后运算结果变成了8个数，这时需要把第7和8位的数去掉。如果直接去掉，会使精度受影响，通常有下边两个方法：
① 0舍1入法：
假设运算结果：X = 0.11010111，假设原本加数和被加数算上符号位一共有6个数，结果X是10个数，那么要去掉后四个数（0111）。由于0111首位是0（即要去掉的数的最高位为0），这种情况下，直接去掉这四个数就可以。该例最后结果为 X = 00.1101
假设运算结果 Y = 00.11001001，这时要去掉的数为1001四个数，由于这四个数的首位为1（即要去掉的数的最高位为1），这种情况下，直接去掉这四个数，再在去掉这四个数的新尾数的末尾加1。如果+1后又出现了溢出，继续进行右规操作。该例最后结果为 Y = 00.1101。
② 置1法
这个比较简单，去掉多余的尾数，然后保证去掉这四个数的新尾数的最后一位为1（即是1不用管，是0改成1）即可。比如 Z=00.11000111，置1法之后的结果为Z=00.11001。
3.5 阶码溢出处理
阶码溢出在规格化和右移的过程中都有可能发生，若阶码不溢出，加减运算正常结束（即判断浮点数是否溢出，不需要判断尾数是否溢出，直接判断阶码是否溢出即可）。若阶码下溢，置运算结果为机器0（通常阶码和尾数全置0）。若上溢，置溢出标志为1。
// 有问题的版本
#include <stdio.h>
int main() {
float sum = 0.0f; // sum是浮点数
for (int i = 0; i < 10000; i++)
sum += i + 1; // 整数i+1会转换为浮点表示，当达到16777215后，浮点表示会有精度丢失
// 1累加到5793会超过16777215
printf("Sum: %f\n", sum); // 50002896.000000
return 0;
}
// 1 + 2 + 3 + … + 10000 = 10000 * (10000 + 1) / 2 = 50005000 ?
// 修正的版本
#include <stdio.h>
int main() {
float sum = 0.0f, corr = 0.0f; /* corrective value for rounding error */
for (int i = 0; i < 10000; i++) {
float y = (i + 1) - corr; /* add the correction to specific item */
float t = sum + y; /* bits might be lost */
corr = (t - sum) - y; /* recover lost bits */
sum = t;
}
printf("Sum: %f\n", sum);
return 0;
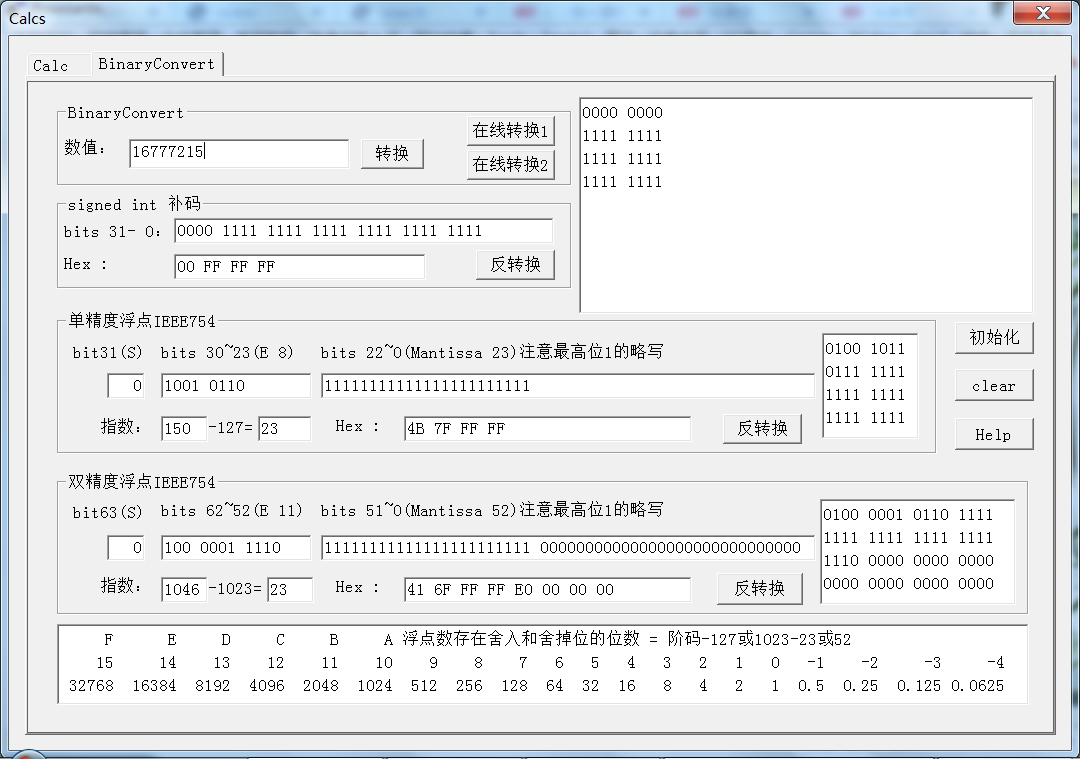
}16777215的浮点表示：
－End－
